算法导论之动态规划笔记

发表于 分类于

第三版 算法导论 - 第四部分 高级设计和分析技术 - 第 15 章 动态规划

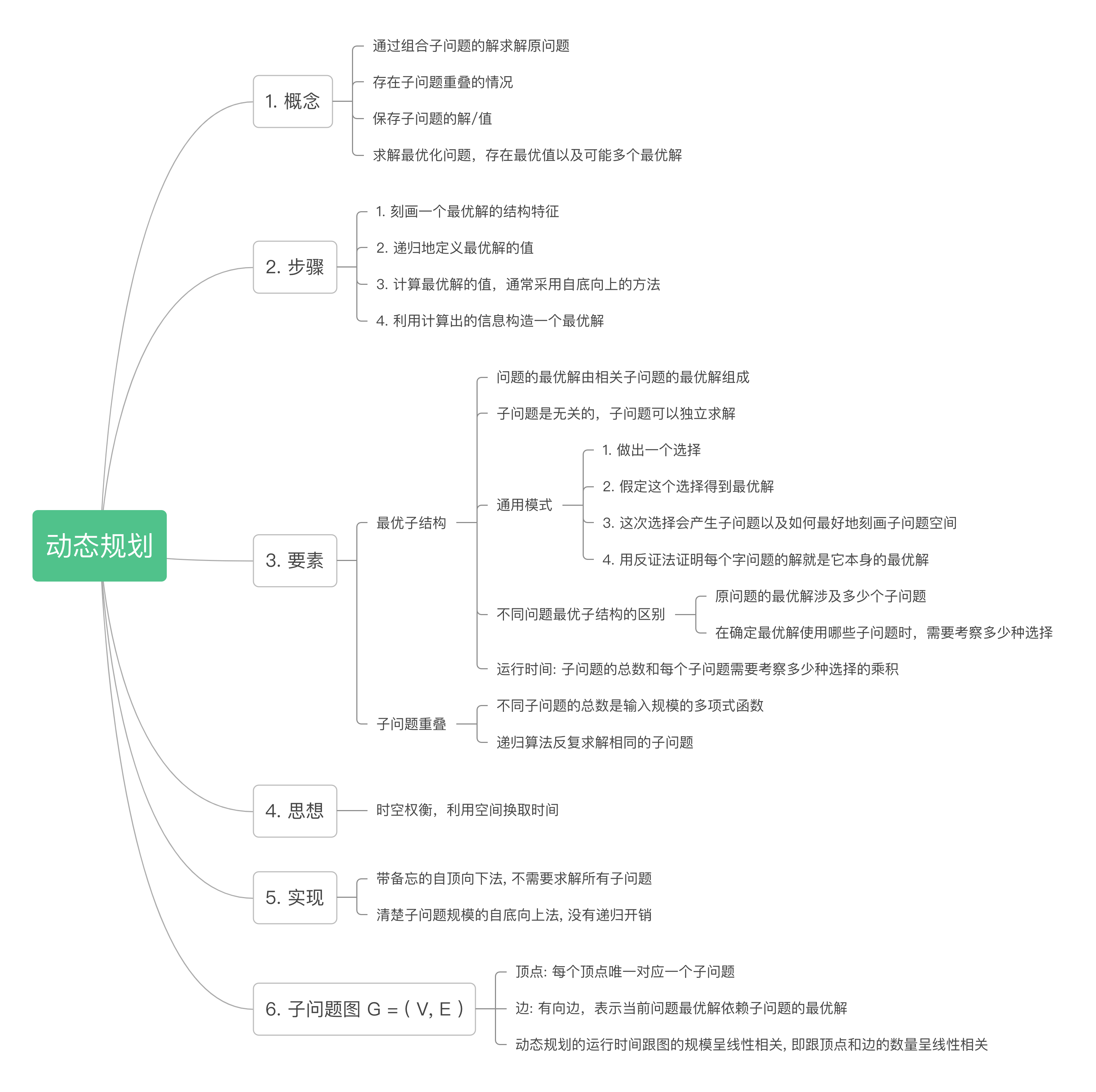
image alt text

  1. 概念

    • 通过组合子问题的解求解原问题
    • 存在子问题重叠的情况
    • 保存子问题的解/值
    • 求解最优化问题，存在最优值以及可能多个最优解

  2. 步骤

    1. 刻画一个最优解的结构特征
    2. 递归地定义最优解的值
    3. 计算最优解的值，通常采用自底向上的方法
    4. 利用计算出的信息构造出一个最优解

  3. 要素

    • 最优子结构
      • 问题的最优解由相关子问题的最优解组成
      • 子问题是无关的，子问题可以独立求解
      • 通用模式
        1. 做出一个选择
        2. 假定这个选择得到最优解
        3. 这次选择会产生子问题以及如何最好地刻画子问题空间
        4. 用反证法证明每个字问题的解就是它本身的最优解
      • 不同问题最优子结构的区别
        • 原问题的最优解涉及多少个子问题
        • 在确定最优解使用哪些子问题时，需要考察多少种选择
      • 运行时间: 子问题的总数和每个子问题需要考察多少种选择的乘积
    • 子问题重叠
      • 不同子问题的总数是输入规模的多项式函数
      • 递归算法反复求解相同的子问题

  4. 思想

    • 时空权衡，利用空间换取时间

  5. 实现

    • 带备忘的自顶向下法, 不需要求解所有子问题
    • 清楚子问题规模的自底向上法, 没有递归开销

  6. 子问题图 G = ( V, E )

    • 顶点: 每个顶点唯一对应一个子问题
    • 边: 有向边，表示当前问题最优解依赖子问题的最优解
    • 动态规划的运行时间跟图的规模呈线性相关, 即跟顶点和边的数量呈线性相关